Regresión Lineal: teoría y ejemplos

Qué es la regresión lineal y qué importancia tiene. Qué tipos de regresión lineal existen. Cómo se aplica un modelo de regresión lineal. Herramientas de software aplicadas en la regresión linear. Ejemplos de cómo se aplica la regresión lineal en la vida cotidiana.

¿Qué es la regresión lineal?

La regresión lineal es un modelo matemático que describe la relación entre varias variables. Los modelos de regresión lineal son un procedimiento estadístico que ayuda a predecir el futuro. Se utiliza en los campos científicos y en los negocios, y en las últimas décadas se ha utilizado en el aprendizaje automático.

La tarea de la regresión en el aprendizaje automático consiste en predecir un parámetro (Y) a partir de un parámetro conocido X.

¿Por qué es importante la regresión lineal?

Los modelos de regresión lineal son muy populares en diversos campos de investigación gracias a su rapidez y facilidad de interpretación.

Debido a su capacidad para transformar datos, pueden utilizarse para simular una amplia gama de relaciones, y debido a su forma, que es más simple que la de las redes neuronales, sus parámetros estadísticos se analizan y comparan con facilidad, lo que permite que se les extraiga información valiosa.

La regresión lineal no sólo se utiliza con fines de predicción: también ha demostrado su eficacia para describir sistemas. Si quieres modelar los valores de una variable numérica, tendrás una lista relativamente corta de variables independientes y, como esperas que el modelo sea comprensible, es probable que elijas la regresión lineal como herramienta de modelización.

Tipos de regresión lineal

Dependiendo de los objetivos del estudio, puedes elegir entre diversos tipos de análisis de regresión:

Simple

En una regresión lineal, se trata de establecer una relación entre una variable independiente y su correspondiente variable dependiente. Esta relación se expresa como una línea recta. No es posible trazar una línea recta que pase por todos los puntos de un gráfico si estos se encuentran ordenados de manera caótica. Por lo tanto, sólo se determina la ubicación óptima de esta línea mediante una regresión lineal. Algunos puntos seguirán distanciados de la recta, pero esta distancia debe ser mínima. El cálculo de la distancia mínima de la recta a cada punto se denomina función de pérdida.

La ecuación de una línea recta tiene la siguiente forma:

Y = β₀ + β₁X + ε,

donde:

1. Y es la variable independiente.
2. β₀ y β₁ son dos constantes desconocidas que representan el punto de intersección y la pendiente respectivamente.
3. ε (epsilon) es la función de pérdida.

A continuación se muestra un ejemplo gráfico de un modelo de una regresión lineal simple:

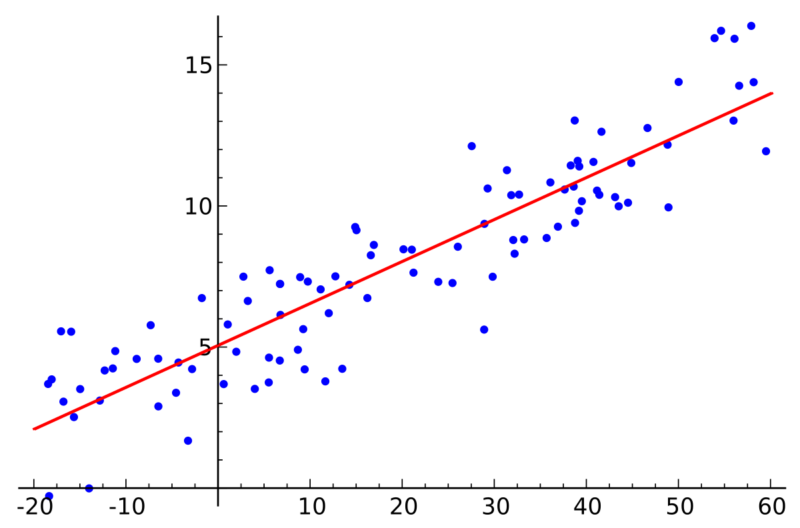
Aplicación de la regresión lineal simple:

1. Para predecir la cosecha en función de la precipitación, con la precipitación como variable independiente y la cosecha como variable dependiente.
2. Para saber qué calificación obtendrán los alumnos en función del número de horas que estudien: aquí la cantidad de horas de estudio representa la variable independiente y las calificaciones, la dependiente.
3. Para prever el salario basado en la experiencia: la experiencia se convierte en la variable independiente y el salario en la variable dependiente.

Limitaciones de la regresión lineal simple:

La regresión lineal simple establece que existe una relación entre las variables, pero no revela una relación causal: Y depende de , pero no implica que genere a Y.

Si necesitas establecer algo más que la existencia de una relación, tendrás que hacer análisis adicionales.

Múltiple

La regresión lineal múltiple encuentra la relación entre dos o más variables independientes y su correspondiente variable dependiente.

La ecuación de regresión lineal múltiple tiene la siguiente forma:

Y = β₀ + β₁X₁ + β₂X₂ +… + βₐXₐ + ε

Donde:

1. Y es la variable dependiente.
2. X es una variable independiente.
3. β son coeficientes.
4. ε (epsilon) es la función de pérdida.

A continuación se muestra un ejemplo de gráfico de un modelo de regresión lineal múltiple:

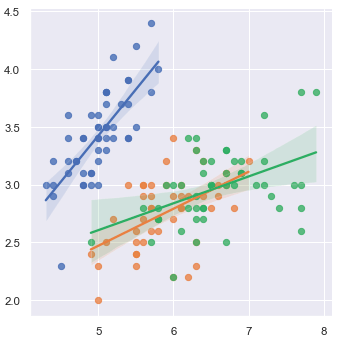
Aplicaciones de la regresión lineal múltiple:

Este tipo de regresión permite predecir tendencias y valores futuros. El análisis de regresión lineal múltiple ayuda a determinar el grado de influencia de las variables independientes sobre la variable dependiente, es decir, cuánto cambiará la variable dependiente cuando cambiemos las variables independientes.

Programas para un análisis de regresión lineal

JASP: Es un excelente software gratuito de análisis de regresión para Windows y Mac. Contiene un módulo de regresión con varios métodos de análisis de regresión. Con ellos puedes analizar fácilmente las variables que afectan a un tema o área de interés.

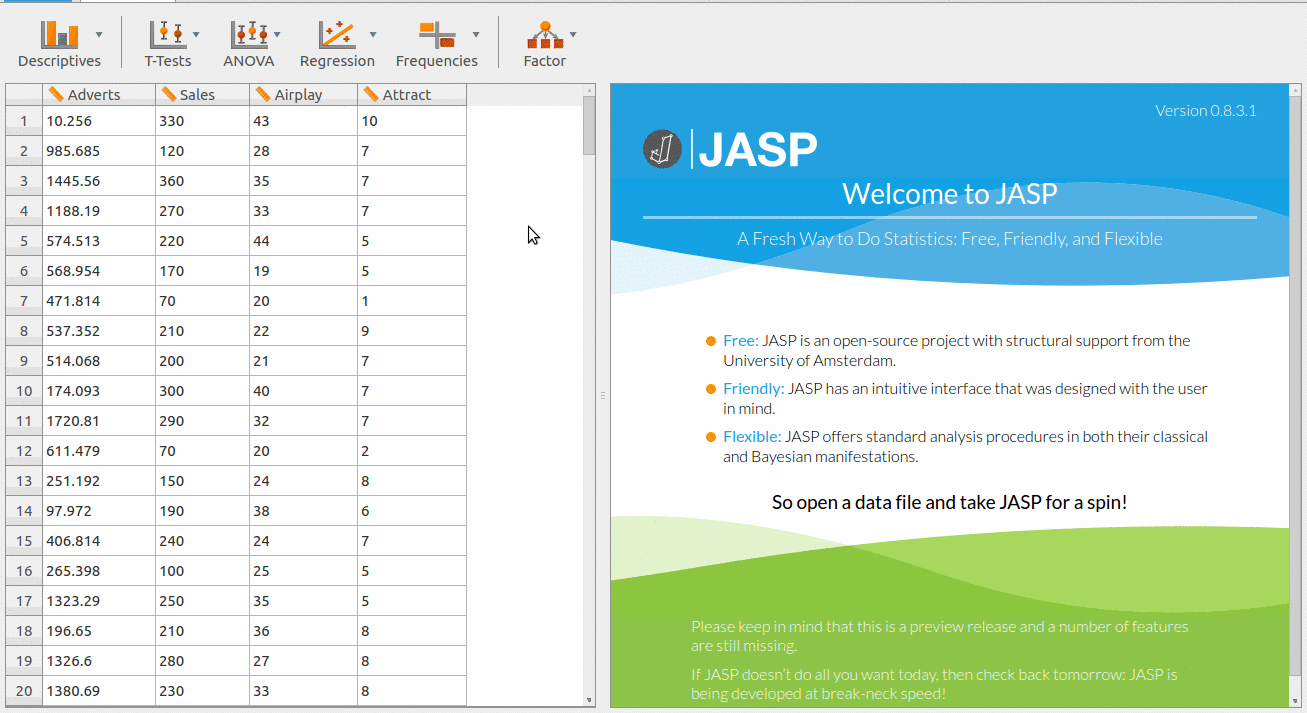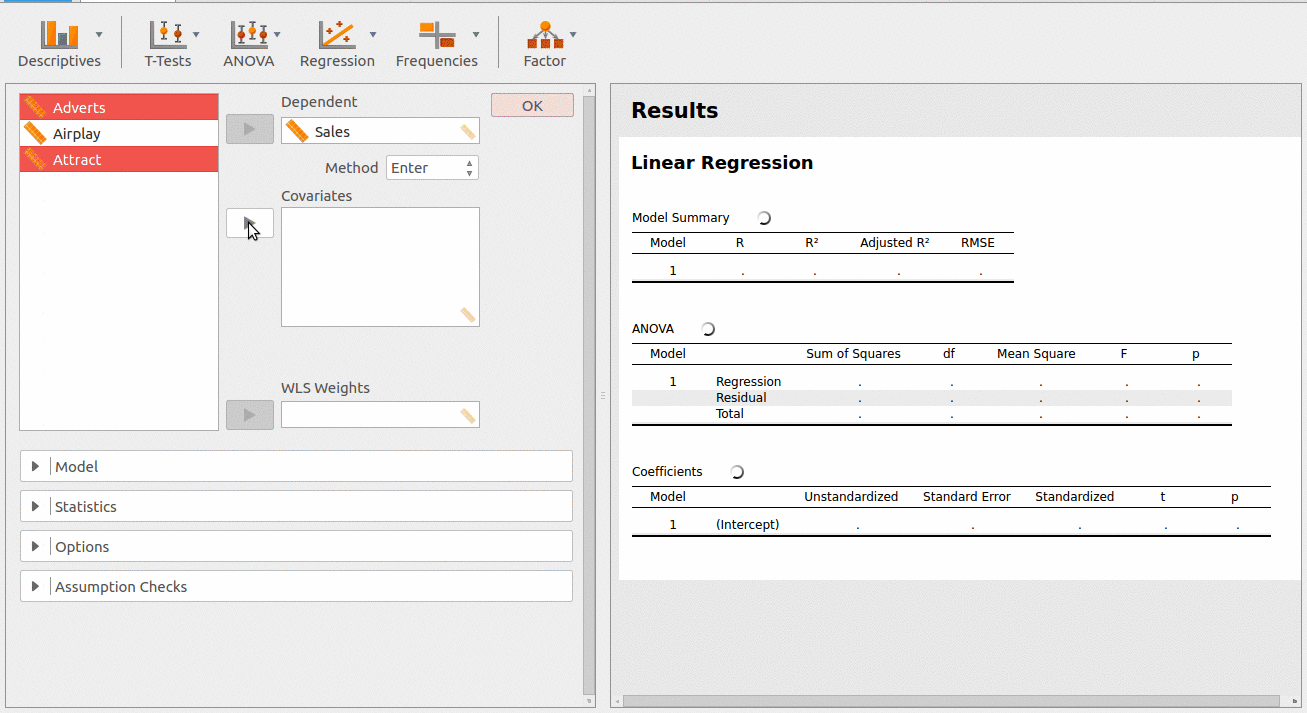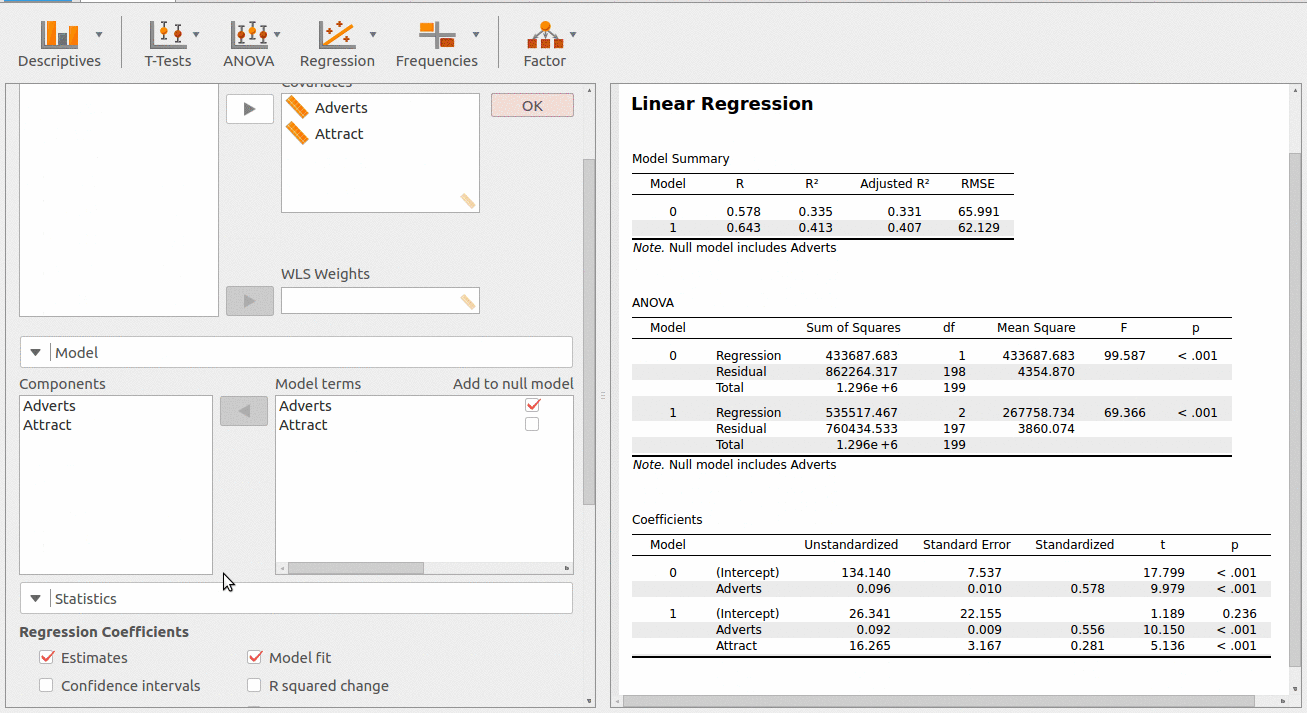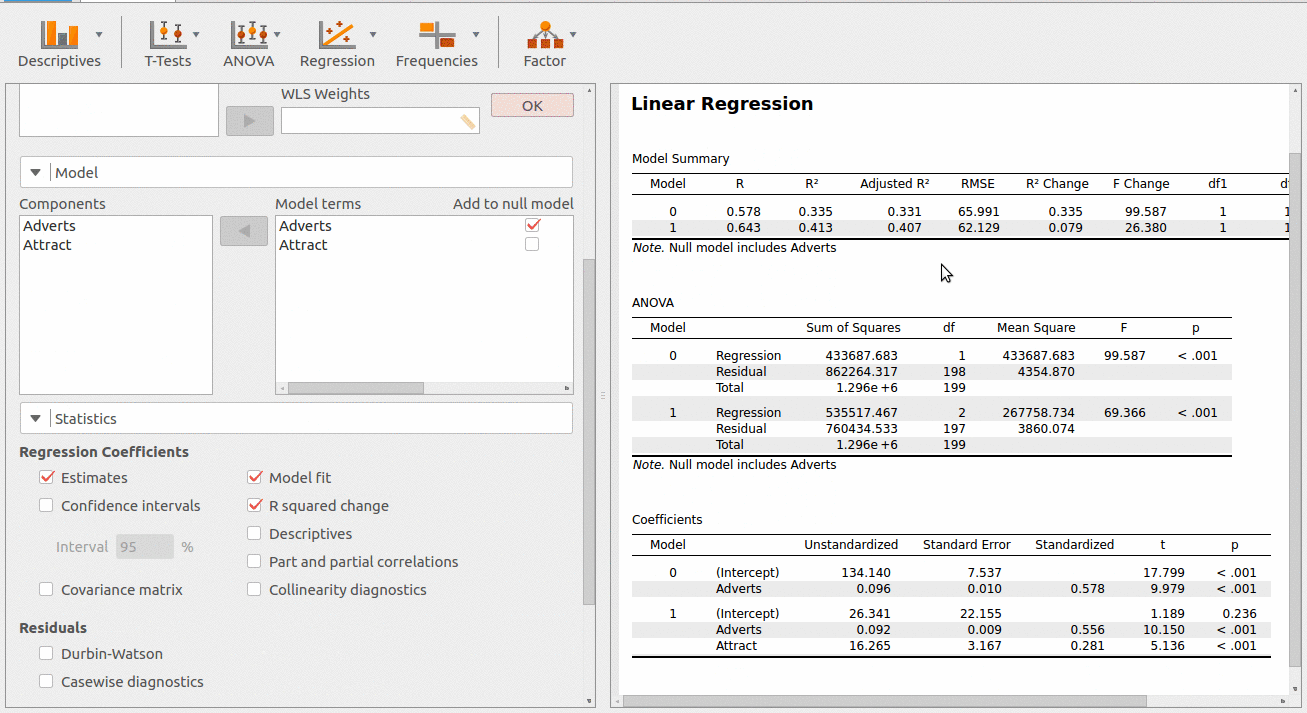
PSPP: Es un software gratuito de análisis de regresión para Windows, Mac, Ubuntu, FreeBSD y otros sistemas operativos. Proporciona métodos de regresión para estimar un conjunto de datos. Puedes introducir fácilmente un conjunto de datos en él y luego realizar un análisis de regresión. Los resultados del análisis de regresión se muestran en una ventana de visualización de resultados con todos los pasos usados.

Statcato: Es un software de análisis de regresión gratuito y portátil basado en Java para Windows, Linux y Mac. Para poder ejecutar este software, es necesario tener instalado Java.

Jamovi: Es otro software gratuito de análisis de regresión para Windows, Linux, Mac y Chrome OS. Es un software de análisis estadístico agradable, conciso y fácil de usar, empleado para tareas relacionadas con el análisis de datos.

Ejemplos de uso de regresión lineal en la vida real

Ejemplo 1. Supongamos que necesitamos entender la relación entre los gastos en publicidad y los ingresos. Representemos esto con un modelo de regresión lineal, en el que la inversión publicitaria es la variable independiente y los ingresos la variable dependiente. El modelo de regresión sería el siguiente:

Ingresos = β₀ + β₁(Gastos en publicidad),

β₀ representa los ingresos totales esperados sin invertir en publicidad.

β₁ es el cambio promedio en los ingresos totales al aumentar el gasto en publicidad en una unidad (por ejemplo, un peso mexicano).

Si el valor de β₁ es negativo, cuanto mayor sea el gasto en publicidad, menores serán los ingresos.

Si el valor de β₁ tiende a cero, significa que la inversión en publicidad tiene poco efecto sobre los ingresos.

Si el valor de ₁ es positivo, cuanto mayor sea la inversión en publicidad, mayores serán los ingresos.

En función del valor de β₁, la empresa puede decidir reducir o aumentar su inversión en publicidad.

Ejemplo 2. La regresión lineal también se utiliza en medicina cuando hay que establecer la relación entre la dosis de los medicamentos y la presión arterial de los pacientes.

Para ello, tomaremos la dosis como variable independiente y la presión arterial como variable dependiente. El modelo de regresión tendrá la siguiente forma:

Presión = β₀ + β₁ (Dosis),

β₀ representa la presión arterial esperada cuando no se suministran medicamentos, la dosis es igual a cero.

β₁ Es el cambio promedio en la presión arterial cuando se aumenta la dosis en una unidad.

Si β₁ es negativo, la presión arterial disminuirá al aumentar la dosis.

Si el valor de ₁ tiende a cero, el cambio en la presión arterial no se debe a un aumento de la dosis del medicamento.

Si el valor de β₁ es positivo, entonces la presión arterial aumentará si se eleva la dosis.

El valor de β₁ permite decidir si se modifica la dosis para el paciente.

Ejemplo 3. Los agrónomos miden el efecto de los fertilizantes y el agua en la cosecha mediante una regresión lineal.

El fertilizante y el agua son la variable independiente y el rendimiento es la variable dependiente. El modelo de regresión será:

Rendimiento = β₀ + β₁ (fertilizante) + β₂,

β₀ indica la cosecha esperada sin usar fertilizantes, ni agua.

β₁ Es el cambio promedio en la cosecha cuando la cantidad de fertilizante se aumenta en una unidad, suponiendo que la cantidad de agua permanece constante.

β₂ Es el cambio promedio en la cosecha cuando la cantidad de agua se aumenta en una unidad, asumiendo que la cantidad de fertilizante es la misma.

En función de los valores de β₁ y β₂, los agrónomos podrán ajustar la cantidad de fertilizante y agua para maximizar la cosecha.

Ejemplo 4. La regresión lineal también puede aplicarse en el deporte: Este método permite determinar el efecto de diferentes sistemas de entrenamiento en el rendimiento de los jugadores.

Por ejemplo, los expertos en Data Science de la NBA pueden analizar cómo afectan al rendimiento de un jugador las distintas sesiones de yoga y de levantamiento de pesas. Tomemos las sesiones de yoga y las sesiones de levantamiento de pesas como variables independientes y el resultado final como variable dependiente. Obtendremos:

Rendimiento = β₀ + β₁ (Sesiones de yoga) + β₂ (Sesiones de levantamiento de pesas),

β₀ representa el rendimiento esperado de un jugador que es vago y no hace ni yoga ni levanta pesas.

β₁ es el resultado promedio que se obtiene al aumentar en uno el número de sesiones semanales de yoga, suponiendo que el número de sesiones semanales de levantamiento de pesas no cambie.

β₂ indica el cambio promedio en el resultado que se consigue al aumentar en uno el número de sesiones semanales de levantamiento de pesas, sin cambiar el número de sesiones semanales de yoga.

En función de los valores de β₁ y β₂, los especialistas pueden recomendar al jugador que aumente o disminuya el número de sesiones de yoga y de levantamiento de pesas para maximizar sus resultados.

Conclusión

La regresión lineal describe la relación entre varias variables: la variable dependiente y una o varias variables independientes. Por su rapidez de creación y su facilidad de interpretación, los modelos de regresión lineal se han utilizado con éxito en diversos ámbitos, desde la medicina hasta la agronomía, tanto para hacer previsiones como para describir sistemas. Existen programas gratuitos que explican cómo hacer para que aplicar el análisis de regresión sea fácil y eficaz.